The Unbearable Weightiness of Tungsten January 1, 2025

Here’s a silly and fun experiment, just because it’s the holidays. You see, tungsten objects are a bit of a meme among a certain segment of the Internet, because they have an impressive heft: tungsten is one of the densest commonly available elements, comparable to gold (but much cheaper, of course). It’s quite enjoyable—in a nerdy sort of way—to hold tungsten objects, which has led some, er, software engineers with too much disposable income to spend hundreds of dollars on featureless metal cubes. To quote a legendary (in my mind) Amazon review on the classic 1.5-inch, 1-kilogram cube:

Nietzsche once said that a man who has a why can bear almost any how. But a man who has a tungsten cube can bear any object less dense, and all this talk of why and how becomes unnecessary.

Schopenhauer once said that every man takes the limits of his own field of vision for the limits of the world. Tungsten expands the limits of a man’s field of vision by showing him an example of increased density, in comparison to which the everyday objects to which he was formerly acquainted gain a light and airy quality. Who can lament the tragedy of life, when surrounded by such lightweight objects? Who can cry in a world of styrofoam and cushions?

Now, I recently got a nice tungsten top as a Secret Santa gift. (Thanks Sivan!) It’s very pleasant to play with, largely because it’s surprisingly heavy given how small it is. But just how dense is it? I wanted to estimate it to find out, and also to prove that I wasn’t cheated and given a lead top instead.

My roommate happens to own a kitchen scale, so finding the mass of the top was pretty easy. I measured it to be $m = 45$ (in grams). Finding the volume, however, turned out to be a bit more involved.

The shape of the top is not very simple, so just measuring it with calipers wouldn’t have been very helpful. The obvious solution here is the old method of Archimedes: place it in a beaker of water, and look at the volume of the displaced fluid. However, I don’t own a graduated cylinder,¹ so this was kind of hard to do. Instead, I settled on computing the volume by integrating over the curve of the top’s surface. Supposing for a moment that we knew the manufacturer’s true curve $f : C \to \mathbb{R}_{\ge 0}$, we’d naturally just compute the volume by taking the integral $$\pi \int_C f(x)^2\,\mathrm{d}x.$$ Of course, I don’t know what $f$ really is, but I figured I could get a decent enough approximation by sampling a bunch of points along the curve. I took a picture of the top next to a ruler,² and then I loaded the image into ImageJ and plotted 99 points along the curve.³

I normalized my points a bit to make the computation a bit simpler: I translated the points to put one end of the top at the origin and then rotated them so that the axis of rotation lay along the $x$-axis, effectively applying the following rigid affine transformation: $$\vec{v} \mapsto \mathrm{Rot}(\theta) (\vec{v} - \vec{v}_0).$$ Then, I scaled the points so that one unit along the $x$-axis was equal to 1 cm. The resulting data:

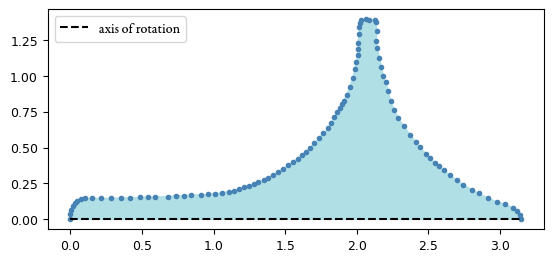
Finally, we can approximate the integral with the classic trapezoidal rule (remember that from AP Calculus?), giving a volume estimate of $$v = \frac{\pi}{2} \sum_{i=0}^{98} \left(y_i^2 + y_{i+1}^2\right) \left(x_{i+1} - x_i\right) \approx 2.408,$$ in cm³. At last, we can simply compute the density the obvious way: $$m / v = 18.685,$$ in g/cm³. This is actually not too bad, keeping in mind the errors we might have accumulated along the way. As a rough estimate of how sensitive this approximation is to errors in the placement of our points, note that perturbing all of the points uniformly away from the axis of rotation by five pixels⁴ (corresponding to about 0.324 millimeters) yields a 9.38% decrease in the density estimate. It’s not great, but it’s at least enough to distinguish between a tungsten alloy and a different dense element like lead.

According to Wikipedia, the density of pure tungsten is 19.254 g/cm³, so our value of 18.685 g/cm³ is well within the realm of plausibility for a tungsten alloy.⁵ For comparison, the density of lead is only 11.348 g/cm³, so we can confidently say that this toy is not made of lead. I’m sorry I ever doubted you, Sivan.

Anyway, this was a fun use of a weeknight, and it was honestly kind of nostalgic, reminding me of my high school days. I used to fancy myself a roboticist (before I was seduced by computer science), and so rotation matrices used to be my friends. The integrals bring back fond memories of Dr. Eng’s multivariable calculus class, and I definitely used ImageJ for some projects. Or maybe I’m just feeling sentimental because it is the holidays, after all.